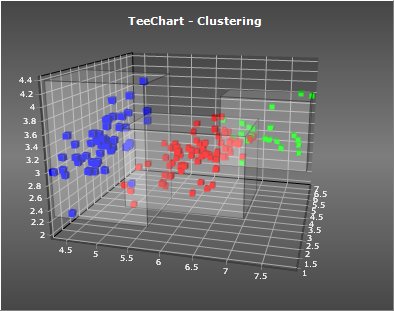
TeeChart Pro includes classes and components to perform “clustering” on your data, and optionally visualize the results using a chart “Tool” component.
Clustering is the process of grouping data automatically, according to how well related are the individual items.
As an unsupervised algorithm, its widely used in data-mining / machine-learning / B.I. (Business Intelligence) applications.
For more information on clustering visit the following Wikipedia link: http://en.wikipedia.org/wiki/Cluster_analysis
An executable example:
http://www.steema.us/files/public/teechart/vcl/demos/clustering/TeeChart_Clustering.zip
The clustering algorithm can be processed on custom data, not necessarily on TeeChart “Series” data.
Classes and Units
The TeeClustering.pas unit, for both VCL and Firemonkey, contains abstract “engine” classes that perform the clustering algorithms.
Three different clustering methods are provided:
• TKMeansClustering
• THierarchicalClustering
• TQTClustering (Quality Threshold)
These classes derive from a common abstract class: TBaseClustering.
Each clustering method has its own properties that determine how will the clusters be calculated. After calculating, you can access the Clusters property, which is a TList of TCluster objects.
A TCluster contains child clusters (Items[ ]), so you can check which input data items belong to which cluster, or in the case of the Hierarchical type, access the tree structure (clusters and sub-clusters).
The input data (your data) is not contained by the above classes.
Data is passed to the clustering engine through a “provider” class. There is currently one kind of data provider (TSeriesProvider) to cluster XY or XYZ Series points.
This class is implemented in the TeeClusteringTool.pas unit, together with a charting Tool class (TClusteringTool) to make things easier and more automatic.
Basic Example
Example runtime code (it can be done at design-time too, without coding) :
uses TeeClusteringTool;
var tool : TClusteringTool;
tool:=TClusteringTool.Create(Self);
tool.ParentChart:=Chart1;
tool.Series:=Series1; // your series
tool.Method:=cmKMeans;
tool.KMeans.NumClusters:=5;
tool.Execute;After execution, you can loop on the resulting output clusters, for example:
var t : Integer;
for t:=0 to tool.Clusters.Count-1 do
Memo1.Lines.Add( 'Cluster: '+IntToStr(t)+' contains: '+
IntToStr(tool.Clusters[t].Count)+' points' );TClusteringTool
This tool automatically performs clustering using the choosen method and parameters, and optionally paints each source series point with a different color indicating which cluster they belong to, and/or draws polygons around each group of cluster’s items, among other things.
Properties:
ClusteringTool1.Method := cmHierarchical;
ClusteringTool1.ColorEach := True; // paint Series with one color per cluster
ClusteringTool1.ShowBounds := True; // draws convex polygons bounding each cluster points
ClusteringTool1.Centers.Visible := True; // shows cluster centers
ClusteringTool1.Centroids.Visible := True; // shows cluster centroids
Other properties include Brush, Pen and Transparency, used when drawing cluster polygon boundaries.Methods:
Several helper methods are provided:
// Obtain cluster's center and centroid XY points in Series scales:
var P : TPointFloat;
P:=ClusteringTool1.GetClusterCenter( ClusteringTool1.Clusters[3] );
P:=ClusteringTool1.GetClusterCentroid( ClusteringTool1.Clusters[2] );
// Obtain an array of XY points (in screen pixel coordinates), that belong to cluster:
var PP : TPointArray;
ClusteringTool1.GetClusterPoints( ClusteringTool1.Clusters[4], PP);
// ...
PP:=nil;
// Get cluster statistics:
var S : TClusterStats;
S:=ClusteringTool1.GetStats( ClusteringTool1.Clusters[0] );Calculation parameters
Each clustering algorithm needs different parameters:
K-Means:
ClusteringTool1.KMeans.NumClusters := 10; // Number of minimum clusters ("K")
ClusteringTool1.KMeans.MaxIterations := 1000; // Maximum number of iterations before stoppingHierarchical:
ClusteringTool1.Hierarchical.NumClusters := 8; // Number of tree root clustersQT:
ClusteringTool1.QTClustering.MinCount := 30; // Minimum number of points to form a cluster
ClusteringTool1.QTClustering.MaxDiameter := 100; // Maximum "diameter" a cluster can growCommon parameters:
Distance
Cluster calculation is based on the “distance” between a data item and the other data items. There are several ways to calculate the “distance” between items.
The algorithms are agnostic, they call the Provider (ie: Series provider) to obtain the distances.
For example, on a XY scatter plot, the distance between points can be for example the hypotenuse (Pythagoras’ theorem), that is, the simple Euclidean distance between a point XY and another XY.
Distance calculations implemented:
dmEuclidean
dmSquaredEuclidean
dmManhattan
dmMinkowski
dmSorensen
dmChebyshev
Example:
ClusteringTool1.Distance := dmMinkowski;
ClusteringTool1.MinkowskiLambda := 4;Linkage
There are several ways to calculate the “distance” between clusters when one or the two clusters have more than one item.
This is called “linkage”.
The most simple way is using each cluster “center” (this means no linkage occurs).
Other linkage styles implemented:
lmSingle
Also called “minimum”.
The distance between cluster A and B is the minimum distance between all items in cluster A and all items in cluster B.
lmComplete
Also called “maximum”.
The distance between cluster A and B is the maximum distance between all items in cluster A and all items in cluster B.
lmAverage
The distance between cluster A and B is the average distance between all items in cluster A and all items in cluster B.
lmWard
The result is the increase on “error sum of squares” when adding cluster B items to cluster A.
Calculation speed
Clustering is a slow process by nature. Each clustering method has different performance bottlenecks, proportional to the number of input data items.
The TeeClustering.pas unit has been greatly fine-tuned to optimize the speed of each algorithm, although much work is needed to find more advanced techniques that require less CPU cycles.
The QT Threshold algorithm benefits of parallelism, when multiple CPUs can be used together.
Speed examples (revisited):
(Time in milliseconds, Windows 8.1 x64 on Intel i7 4770 @ 3.4Ghz)
IDE XE8 Delphi, Win32, 5000 data points
| Algorithm | Single CPU | Multiple CPU |
| K-Means | 47 | 31 |
| Hierarchical | 4328 | 4156 |
| QT | 2859 | 703 |
Notes:
x64 bit executables are a little bit faster than 32bit.
Speed is also very dependant on the “distance” calculation method that is used to compare data. The default Euclidean calculation has a quite big CPU cost as it calculates the Hypotenuse between two data XY value pairs.
Very nice implementation of this very useful multivariate data analysis technique. With its use of XY (2D) or XYZ (3D) data the current implementation is great for the analysis of spatial / GIS type problems. However with the amount of work already done it would be relative easy to transform the current implementation into a truly multivariate analysis system. I would guess that currently 90-95% of the work required is already done. Distance calculations would need to be extended to a generic N-dimensional approach. And to be able to compare measurements that are of (vastly) different scales one or more normalization methods (i.e. z-scores) would be required. In the past I wrote a similar K-Means clustering program in Delphi for geo-scientific applications. If people are interested I am willing to share what I know (including code & executable) on the subject.
Hi Jan, thanks a lot for your comments. We have a new version in the works, that works with N-dimensions. The XY and XYZ limit is because the current code was oriented to display the data. We can send you the full code and demos if you want to take a look. Normalization is also a planned feature.
regards !
david
The Clustering demo code is included with the TeeChart Feature Demo:
https://github.com/Steema/TeeChart-VCL-samples/tree/master/TeeNew
Impressive article on clustering visualization……………was of great help keep posting